Do you do Su-Do-Ku?
Su-do-ku is a number puzzle that has recently appeared in newspapers, books, and elsewhere. It's popularity is said to be large and growing.
For those of you unfamiliar with it, it consists of a square divided into 9 subsquares, each of which is further divided into 9 subsquares of its own for a total of 81 little squares. Some of the squares contain numbers.
The puzzle can be found in several configurations from difficult to damn near impossible.
The mission, should you choose to accept it, is to fill in the blank squares so that each horizontal row, each vertical row, and each of the nine subsquares all contain the numbers 1 through 9.
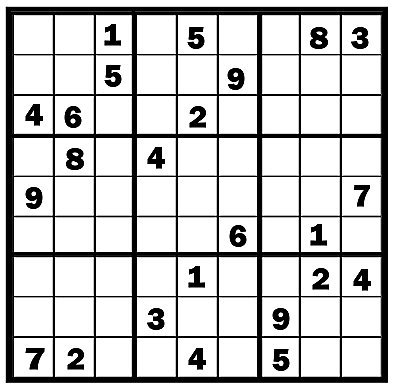
I'd seen these puzzles mentioned in various places, and today I decided to give it a try for the first time. I've been grinding on it for hours, but it's got me stymied.
I initially decided to go through each blank square and pencil in all the possible numbers for that square. That took a fairly long time in itself.
I was then able to find a couple rows and columns where a number only occured once, so therefore that square had to be that number.
But after that, I was stopped in my tracks. Now I'm left with many squares with many possible numbers.
My plea is to anyone who has experience with these fascinating puzzles to let us know if there's a method to this madness. Is there a system or process you use?
I'd be eternally grateful, as the only way forward from here that I can think of so far is to guess at a number and go from there. Of course, every time you enter a number, it affects the row, column, and subsquare it's in, so it's not as easy as it may sound.
I know there's some extremely bright readers out there and I'm hoping someone can give me some hints or tips. In a word: HELP!!!!
UPDATE: I finally solved the little sucker, but there has GOT to be a better way. I haven't erased that much since grade school. Maybe after you do a few times it becomes easier, but the way I did it was insane.
There's no one choice for several squares, ( in other words, there may be three squares in which you need to fill 5, 6, and 7, but all of them would work in any of the squares.) which forces you to just pick a number and a square. But that choice affects about 15 other squares. So you go along and fill in those squares until it becomes apparent that something doesn't work. But you can't change the problem square, because that impacts on a row and column and subsquare, so.... it's erase all this stuff and start again.
There's hundreds of possible permutations, and it just gets out of hand.
Until you happen to get lucky and make a few correct guesses, it's a nightmare.
Any further hints or tips would be appreciated.
(The solution to the puzzle above is available if anyone needs it. Just send e-mail or tell me in comments and I'll either publish it here or get it to you somehow.)















10 Comments:
The key is to find patterns. In each 3 square column (the first, second, and third third of the puzzle) there can only be one number per column. For example in the middle section. You can see that the four is in the first column in square two, and it is in the second column of square three. Therefore, it has to be in the third column of square one. Now, there are only two open spots on column three of square 1. We can see that four can’t go in the last spot, since there is already a four in that row. So, it has to go on the first spot open.
Also, when you have a row or column nearly full, it is easy to find the numbers missing; since, there has to be 1 through 9. If you have two squares missing out of a row you can find what those two numbers have to be.
Using these two patterns, you can usually solve any puzzle thrown at you... if you can decipher what I just typed.
Scott, not to worry, your comment makes perfect sense. I hadn't come up with the first strategy and will see how it works. Thanks!
The one you posted is pretty tough, I haven't solved it yet.
My parents insist that you aren't ever supposed to get to a point where you have to guess, but I think they're wrong.
QCI,
That's just it. I have a nagging feeling that there's got to be a better way, or that I'm missing something. They can't possibly require all the fooling around I ended up doing.
I'm thinking there has to be some sort of patterns one looks for, or some process of elimination, but I sure couldn't find it.
As I said, I started by jotting in all the possible numbers that could go in each little square. About three of these ended up being only one, which helped.
But from that point on, there were always mulitiple choices, at least to get it going.
Once I made the right guesses at a couple squares, then I could (very carefully) proceed, but unfortunately, after filling in over half the squares, something wouldn't work and I'd have to start again.
FINALLY, I must have picked the correct first couple of guesses, as I was able to slowly pick my way through and solve it.
Let me know if you'd like to see the solution.
QCI,
That's a good idea, of course, but I had already done that before I even put up this post.
I did the thing where I jotted down all the possible numbers in the squares, and then looked for any rows or columns where a number only appeared once. (I don't recall, but it was 1 or maybe 2 at most)
It was at THAT point that I was forced to guess.
If you're working on the one shown, you'll come to the same place at some point.
There'll be two boxes which can be either 6 or 7 in the top row, for instance.
Try plugging them in one way, and it might work, or it might not. (even if you have them right, it might end up not working in other areas, as there are several spots which you have two numbers to fill in and both squares could be either number.)
I'm still looking for some further method to the madness.
Psst... Dope...
That previous post wasn't me,
But I do use that same strategy.
The QCTimes has been pushing Sudoku for a while now, so I'm guessing you're more of a Dispatch man yourself.
Oh man. I'm losing it. Sorry about the mix up QCI. (and highxlr8r)
At any rate, I'm not sure I'd say I'm a "Dispatch man", as I tend to switch back and forth and I read both. But I do tend to check the Dispatch more than the QCT as it has a bit more focus on the IL side of things.
As I said, I've been aware of this So-du-ku thing for some time, but just never had the chance or desire to try it until the other day.
I did my second one last night, and it was considerably easier than the first. MUCH smoother with no "do-overs".
I have a method of sorts now, though it involves having to construct an entire game grid on a separate piece of paper so I have room for all the numbers I have to mark down.
That's a lot of effort which probably isn't needed I suspect.
I still rely on having to jot down all the possible numbers for each square and then cross them off as numbers become solid.
Anyone have a method which doesn't require that?
Someday maybe I'll learn how to do it in the space in the paper. I'm sure it's possible.
I may be wrong, but I have the feeling that there's got to be a simpler and more logical way to solve the things than the way I'm going about it.
I pretty much do the same "cram tiny numbers into empty boxes" thing on the puzzles I can't solve without doing that. I'd say I end up doing it on about a third of the puzzles, and it USUALLY shows me something I've missed. I still haven't solved the one posted above, but I haven't worked on it after the first effort.
Also after filling in the available options, look for pairs of same numbers in any Box or Column or Row. For example, if 5&6 (on their own without any other number) appears in two squares of the same column you can omit 5 & 6 as options from othe squares in the same column. Ditto for a row or a column as applicable.
The best resolver programme that I have found that will also teach you, take out the drudgery and provide hints when you are stuck, is at http://angusj.com/sudoku/ where you can get a quick free download.
It is excellent. You can also enter numbers from say a newspaper and it will help you. Try it.
Post a Comment
<< Home